Теория электрической связи

4. Математические модели случайных процессов

Сигналы в системах передачи информации и действующие в них помехи по своей природе являются случайными процессами. Для их описания необходимо применять математический аппарат теории вероятностей и случайных процессов. Настоящую главу следует рассматривать как развитие раздела 2. Математические модели сигналов (Теория электрической связи. Конспект лекций. Часть 1) применительно к случайным процессам.

4.1. Понятие случайного процесса

xk(t)

x1(t) x2(t)

ti t

Рис. 4.1. Реализации процесса X(t)

Случайный процесс (СП) X(t) является функцией времени, значения которой в любой фиксированный момент времени ti представляют собой случайную величину X(ti). Здесь и в дальнейшем случайные величины и функции будем обозначать заглавными буквами, а детерминированные (неслучайные) – строчными, как это широко принято. На рис. 4.1 изображены возможные реализации x1(t) и x2(t) случайного процесса X(t), являющиеся детерминированными функциями времени. Сам процесс можно трактовать как множество (в том числе и несчетное) подобных реализаций { xk(t) } с соответствующей вероятностной мерой.

Для полного описания сечений X(ti) СП необходимо указать законы распределения значений СП в этих сечениях. Они могут быть заданы в интегральной (функция распределения) или дифференциальной (плотность вероятности) формах. В таблице 4.1., в порядке напоминания, приведены основные сведения об этих законах и их свойствах.

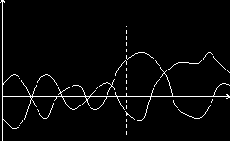
Таблица 4.1

Название и обозначение	Функция распределения F(x)	Плотность вероятности w(x)
Определение
Физическая размерность	безразмерная	размерность
Взаимосвязь
Особенности функции	F(x2)³ F(x1) при x2 > x1 (неубывающая)	w(x)³0 (неотрицательная)
Расчет вероятности
Свойство нормировки

Примеры распределений случайных величин:

Равномерное

Нормальное (гауссовское)

Распределение дискретной случайной величины

                               F(x)

                      1



                                                       x

        x1       x2      x3      x4

                          w(x)

                                                       x

       x1       x2      x3      x4

Информация о сечениях СП не является достаточной для описания самого СП, так как не содержит сведений о зависимостях сечений между собой. Исчерпывающее описание СП осуществляется с помощью n-мерной функции распределения

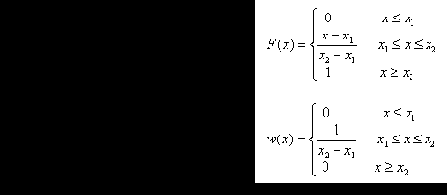
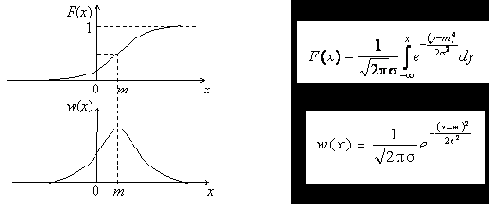
или n-мерной плотности вероятности

,

где x1, x2…, xn – аргументы, t1, t2…, tn – параметры этих функций, а n – любое целое число.

Если n-мерная функция распределения (плотность вероятности) СП не меняется при сдвиге всех моментов tk (k = 1, 2, …, n) на один и тот же интервал Dt, то такой процесс называют стационарным в узком смысле.

4.2. Сокращенное описание случайных процессов

Полное описание СП не всегда возможно, да и не всегда требуется. Во многих случаях достаточно знать основные его характеристики. В качестве таковых широко используют:

1. Математическое ожидание СП – начальный момент первого порядка

2. Дисперсия СП – центральный момент второго порядка

Здесь использовано понятие центрированного СП

.

3. В общем случае можно использовать моменты k-го порядка:

начальные

,

центральные

.

Нетрудно видеть, что моменты полностью определяются одномерным распределением и в общем случае произвольного СП являются детерминированными функциями времени. Для стационарных в узком смысле СП моменты от времени не зависят.

1. Корреляционная (автокорреляционная) функция – центральный смешанный момент второго порядка

.

Случайные процессы называют стационарными в широком смысле, если выполняются следующие условия:

, где ? = t2 – t1

Очевидно, что стационарность СП в узком смысле влечет его стационарность в широком смысле, но не наоборот.

Некоторые свойства корреляционной функции СП:

1.

Доказательство:

,

откуда следует вышеуказанное неравенство

3. Корреляционная функция характеризует статистическую связь сечений СП (внутри процесса). Если связи между сечениями

нет (сечения статистически независимы), то

.

Доказательство:

.

Отсутствие связи влечет отсутствие корреляции, но не наоборот. Обратное утверждение справедливо лишь в случае нормального (гауссовского) процесса.

Нормальным называют СП, у которого одномерная плотность вероятности имеет вид

,

где

,

а любая n-мерная плотность вероятности описывается выражением

,

где An, cij, ai, aj – константы, определяемые выбором сечений t1,t2,,,tn.

4. Корреляционная функция стационарного случайного процесса является четной

.

Доказательство:

.

Подставляя

, получим

.

5. Чтобы абстрагироваться от дисперсии и учитывать только связи внутри СП удобно пользоваться нормированной функцией корреляции (коэффициентом корреляции)

.

Очевидно, что

.

6. Интервал корреляции – грубую числовую оценку связи внутри СП – чаще всего определяют методом равновеликого прямоугольника

.

7. Взаимная корреляционная функция двух процессов X(t) и Y(t)

.

8. Корреляционная функция суммы независимых случайных процессов

есть сумма корреляционных функций каждого из слагаемых СП в отдельности

Доказательство:

Вместо усреднения по множеству реализаций случайного процесса можно ввести его усреднение по времени, определяя:

- постоянную составляющую СП,

- переменную составляющую СП,

- мощность переменной состав-

ляющей СП.

Нетрудно видеть, что эти характеристики являются случайными величинами, не зависящими от времени.

Случайные стационарные процессы называют эргодическими, если их усреднение по множеству и по времени приводит к одинаковым результатам:

Эргодическое свойство СП заключается, грубо говоря, в том, что все его реализации «похожи» друг на друга. Отсюда следует возможность получения вышеуказанных характеристик эргодического СП усреднением по времени единственной его реализации x(t), что существенно облегчает построение аппаратуры для их измерений. В частности, функцию корреляции эргодического СП можно вычислить по одной реализации с помощью следующего выражения:

из которого вытекает схема коррелометра, приведенная на рис. 4.2.

4.3. Спектральный анализ случайных процессов

Спектральный анализ детерминированных сигналов x(t) предпо-лагает использование прямого преобразования Фурье

.

Распространение этого подхода на случайные процессы наталкивается на ряд серьезных проблем:

1.

существует только для функций x(t), удовлетворяющих условию абсолютной интегрируемости

или хотя бы интегрируемости в квадрате

,

т.е. для сигналов с ограниченной энергией. Однако реализации стационарных случайных процессов с вероятностью 1 имеют бесконечную энергию, так как по определению существуют на бесконечной оси времени и, следовательно, этим требованиям не отвечают. Эту трудность можно обойти, если рассматривать отношение спектральной функции

к длительности сигнала Т. Тогда достаточным будет требование ограниченной мощности сигнала x(t)

.

2. Спектральная функция

характеризует отдельные реализации x(t) случайного процесса X(t), а не сам процесс целиком. Попытка перейти, как обычно, к усреднению по ансамблю оказывается несостоятельной. Действительно, если определить математическое ожидание случайной спектральной функции

,

где

- амплитудный, а

- фазовый спектры случайного процесса X(t), то для независимых

при равномерном распределении

в интервале

получим нулевой результат усреднения для ненулевых процессов.

Выход из этой ситуации состоит в отбрасывании фазового и усреднении только амплитудного спектра

или

.

Для реализаций случайных процессов X(t) с ограниченной энергией Ех (нестационарных) по теореме Парсеваля имеем

,

где

- спектральная плотность энергии реализации x(t).

Усредняя по ансамблю реализаций, получим

– спектральную плотность энергии случайного процесса X(t) с размерностью

, что соответствует размерности

, если иметь в виду действие X(t) на сопротивлении 1 Ом.

Для стационарных случайных процессов на интервале Т рассмотрим функцию

, имеющую размерность

. Переходя к пределу при

, получим спектральную плотность мощности

, (4.1)

называемую также энергетическим спектром процесса X(t).

Энергетический спектр стационарного случайного процесса и его корреляционная функция связаны между собой интегральными преобразованиями Фурье, что было строго доказано А.Я. Хинчиным и Н. Винером (теорема Винера-Хинчина)

, (4.2)

. (4.3)

Рассмотрим нестрогое доказательство этой теоремы с прозрачным смыслом. Исходя из вышеприведенного определения энергетического спектра, имеем

(после замены переменных

)

(после замены усреднения по ансамблю усреднением по времени)

,

что и требовалось доказать.

Свойства энергетических спектров случайных процессов

1.

, что непосредственно следует из его определения (4.1). Из этого факта и соотношения (4.3) вытекает важное следствие для корреляционной функции

– она является положительно определенной, т.е. имеет неотрицательное преобразование Фурье.

2.

– четная функция.

.

На этом свойстве основано понятие одностороннего энергетического спектра, существующего только в области положительных частот

.

3.

5. Нормированный энергетический спектр

.

Примеры энергетических спектров некоторых стационарных СП:

1. Квазибелый шум NF(t)

Энергетический спектр такого процесса (

) равномерен в ограниченной полосе частот (–F, +F) (рис. 4.3).

Корреляционная функция квазибелого шума имеет вид (рис. 4. 4)

Из полученного результата вытекает некоррелированность отсчетов квазибелого шума, взятых через интервалы времени k/2F. Для нормального процесса эти отсчеты оказываются еще и независимыми.

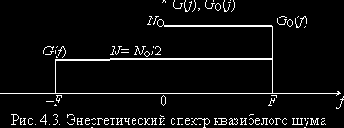
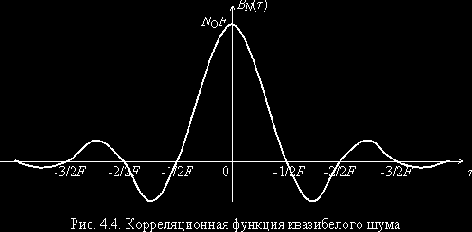
2. Белый шум N(t)

Энергетический спектр белого шума (

) равномерен в бесконечной полосе частот (рис. 4.5).

Корреляционная функция белого шума (рис. 4.6)

,

здесь использовано одно из определений дельта-функции

Из этих результатов вытекает статистическая независимость любых сколь угодно близких сечений такого процесса и его неограниченная дисперсия (мощность)

.

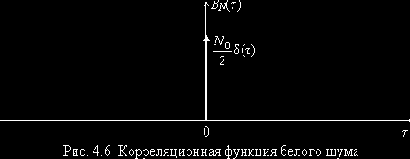
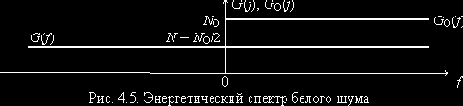
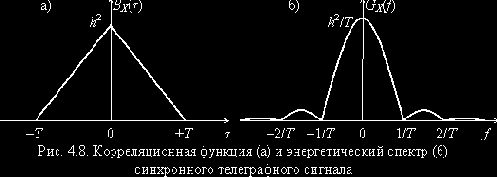
3. Синхронный телеграфный сигнал X(t)

Синхронный телеграфный сигнал (CТС) представляет собой стационарный дискретный случайный процесс, принимающий на тактовых интервалах длительностью Т значения +h с вероятностью Р(0) или –h с вероятностью Р(1). Возможная реализация такого процесса показана на рис. 4.7.

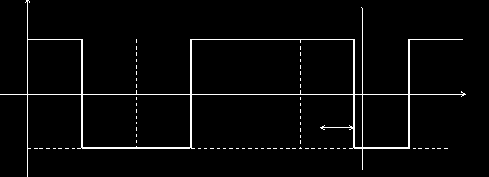
Вычислим корреляционную функцию СТС, исходя из ее определения

,

где

.

В силу стационарности и при Р(0) = Р(1) = 0,5 имеем

= 0 и

Далее учтем, что произведение

, если

, где

временной интервал от сечения t1 до ближайшей границы такта (сечения принадлежат одному тактовому интервалу). В противном случае (при

)

,

где Р(0/0), Р(0/1), Р(1/0) и Р(1/1) – переходные вероятности передачи символов в соседних тактовых интервалах, которые будем считать одинаковыми.

Таким образом

,

где

– плотность вероятности временного интервала

. Окончательно, учитывая свойство четности корреляционной функции стационарного процесса, получим

.

По полученной корреляционной функции несложно рассчитать энергетический спектр синхронного телеграфного сигнала (4.2)

Графики корреляционной функции и энергетического спектра синхронного телеграфного сигнала приведены на рис. 4.8.

Контрольные вопросы

1.     Дайте определение случайного процесса (СП).

2.     Каким образом дают исчерпывающее описание произвольного СП?

3.     Каков смысл и размерность n-мерной функции распределения СП?

4.     Каков смысл и размерность n-мерной плотности вероятности СП?

5.     Как связаны функция распределения и плотность вероятности между собой?

6.     Дайте определение математическому ожиданию СП и укажите его размерность и сущность как математического объекта.

7.     Дайте определение дисперсии СП и укажите ее размерность и сущность как математического объекта.

8.     Как осуществляют центрирование СП?

9.     Определите функцию корреляции СП.

10. Какие СП называют стационарными в широком и узком смыслах?

11. Какие СП называют эргодическими?

12. Дайте определение постоянной составляющей СП, укажите ее размерность и сущность как математического объекта.

13. Дайте определение мощности СП, укажите ее размерность и сущность как математического объекта.

14. Какие СП называют нормальными (гуссовскими)?

15. Что понимают под временем корреляции СП?

16. Укажите основные свойства корреляционной функции стационарных СП?

17. Дайте определение спектральной плотности энергии СП и укажите ее размерность.

18. Дайте определение спектральной плотности мощности (энергетическому спектру) СП и укажите ее размерность.

19. Каковы связи между корреляционной функцией и энергетическим спектром стационарных СП?

20. Укажите основные свойства энергетического спектра стационарных СП.

21. Какой СП называют белым шумом? Укажите основные его свойства.

22. Какой СП называют квазибелым шумом? Укажите основные его свойства.

23. Какой СП называют синхронным телеграфным сигналом? Какова его корреляционная функция?

24. Как выглядит энергетический спектр синхронного телеграфного сигнала?

Рекомендации по проведению экспериментальных

исследований случайных процессов

Для закрепления полученных при изучении раздела 4 знаний на базе виртуальной лаборатории можно провести экспериментальные исследования случайных процессов используя:

осциллограф – для наблюдения реализаций СП во временной области,
анализатор спектра – для наблюдения реализаций СП в частотной области,
анализатор уровней – для наблюдения плотности вероятности,
коррелометр – для наблюдения корреляционных функций.

Целесообразно работать в рамках конфигурации лабораторного стола по темам работ №2 и №19. Источником СП с равномерным и нормальным распределением может служить генератор сигнала (в режиме генератора шума) (рис. 4.9) и соответствующие подпункты меню «Сигналы» (рис. 4.10).

Рекомендуется выполнить лабораторную работу №19 в полном объеме (рис. 4.10). Обратите внимание на связь размеров «шумовой дорожки» на экране осциллографа с эффективным значением шума и на связь корреляционных характеристик с энергетическими спектрами случайных процессов.

5. Прохождение случайных процессов через

преобразователи сигналов

В общем случае решение задачи прохождения заданного СП через конкретную электрическую цепь – функциональный узел (ФУ) произвольной сложности предполагает определение n-мерной плотности вероятности (или функции распределения) реакции цепи Y(t) на заданное случайное воздействие X(t) (рис. 5.1). Однако общего метода решения такой задачи не существует. Поэтому ограничимся рассмотрением некоторых частных случаев.

5.1. Прохождение случайных процессов

через безынерционные цепи

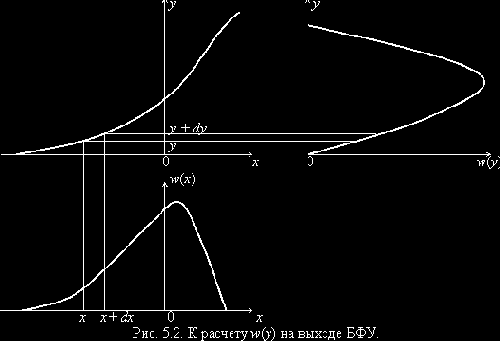
Безынерционная цепь (безынерционный функциональный узел –БФУ) полностью описывается функциональной зависимостью y = f(x), связывающей мгновенные значения воздействия x(t) и реакции y(t) в совпадающие моменты времени. В результате имеем дело с функциональным преобразованием случайного процесса Y(t) = f [X(t)].

Для вычисления одномерной плотности вероятности реакции w(y) по известной плотности вероятности воздействия w(x) рассмотрим рис. 5.2, на котором изображены функциональная характеристика БФУ y = f (x), заданная плотность вероятности воздействия w(x) и искомая плотность вероятности реакции БФУ w(y).

Учитывая, что при попадании случайной величины X в интервал (x, x+dx) случайная величина Y с вероятностью 1 попадает в соответствующий ему интервал (y, y+dy), можно написать следующее соотношение

,

из которого вытекает

, (5.1)

где f -1(y) – обратная функция (x = x(y) = f -1(y)).

Дифференциалы dx, dy и производная обратной функции в полученном выражении взяты по модулю в силу свойства положительности плотности вероятности.

Примеры:

1. Линейное безынерционное преобразование y = f (x) = ax + b.

Обратная функция

.

Таким образом, при линейном преобразовании случайной величины ее кривая плотности распределения смещается на величину b, а масштаб по координатным осям изменяется в |a| раз.

2. Кусочно-линейное преобразование y = f (x) (рис. 5.3).

Задачу решим графически, определяя вид кривой wY(y) на отдельных интервалах оси у.

y y

                                       y2



                                   y1

                                        x1          x2         x              0                                             w(y)

                                            w(x)

                                       x1          x2                              x

Рис. 5.3. Кусочно-линейное преобразование случайной величины.

Из рассмотрения функциональной характеристики y = f (x) с очевидностью вытекает, что

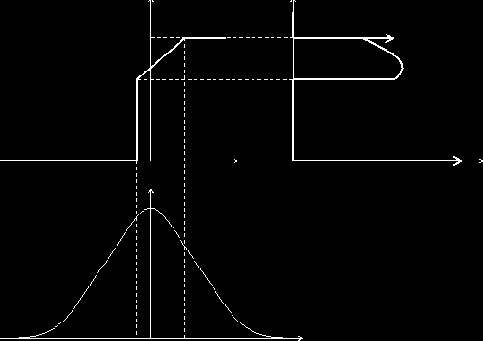
а) при у < 0 и у > y2 wY (y) = 0, т. к. значения реакции у не могут выйти за пределы уровней отсечки (у = 0) и насыщения (у = y2,);

б) при 0 < у < y1 wY (y) = 0, т. к. в этот интервал ( протяженностью y1) значения реакции попадают при единственном значении воздействия x = x1, вероятность которого wX(x1)dx ® 0;

в) при y1 ? у < y2

, где b = y1,

(см. пример 1);

г) при у = 0

, т. к. у = 0 для всех х < x1;

д) при у = у2

, т. к. у = у2 для всех х > x2.

3. Преобразование при неоднозначной обратной функции

.

На практике встречаются ситуации, когда обратная функциональная характеристика является многозначной (рис. 5. 4). Рассуждая аналогично тому, как это делали при выводе выражения (5.1), легко убедиться в том, что в этом случае для интервала

Если при анализе прохождения СП через БФУ достаточно знать только основные характеристики распределения реакции, то их можно найти, не определяя wY(y). В частности:

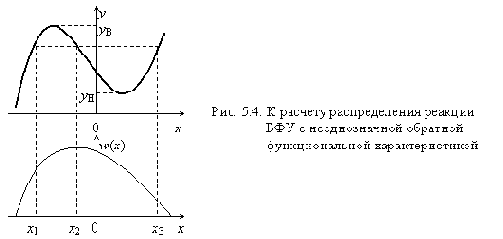
математическое ожидание

,

дисперсия

функция корреляции

.

Функциональное преобразование двух случайных процессов

Постановка задачи:

Заданы два случайных процесса X1(t) и X2(t) с известной совместной плотностью вероятности их значений в совпадающие моменты времени w(x1, x2; t). С этими процессами связаны два других СП Y1(t) и Y2(t) известными функциональными зависимостями

.

Требуется определить w(у1, у2; t) – совместную плотность вероятности процессов Y1(t) и Y2(t) в совпадающие моменты времени.

Решение:

По аналогии с (5.1) можно написать следующее соотношение

,

где J – якобиан преобразования переменных x1, x2 в у1, у2

. (5.2)

5.2. Прохождение случайных процессов через линейные цепи

Общей процедуры определения закона распределения реакции линейного ФУ на произвольное случайное воздействие не существует. Однако, возможен корреляционный анализ, т. е. расчет корреляционной функции реакции по заданной корреляционной функции воздействия, который удобно проводить спектральным методом по схеме, показанной на рис. 5.5.

Для вычисления энергетического спектра GY(f) реакции линейного ФУ с передаточной функцией H(j?) воспользуемся его определением (4.1)

.

Функцию корреляции BY(t) определим преобразованием Фурье энергетического спектра GY(f)

.

Вернемся к определению закона распределения реакции линейного ФУ в отдельных частных случаях:

1.     Линейное преобразование нормального СП порождает также нормальный процесс. Измениться могут только параметры его распределения.

2.     Сумма нормальных СП (реакция сумматора) есть также нормальный процесс.

3.     При прохождении СП с произвольным распределением через узкополосный фильтр (т.е. при ширине полосы пропускания фильтра DF существенно меньшей ширины энергетического спектра воздействия DfX) наблюдается явление нормализации распределения реакции Y(t). Оно заключается в том, что закон распределения реакции приближается к нормальному. Степень этого приближения тем больше, чем сильнее неравенство DF << DfX (рис. 5.6).

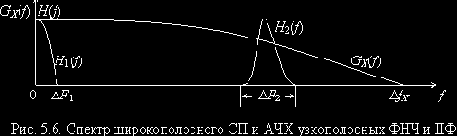
Объяснить это можно следующим образом. В результате прохождения СП через узкополосный фильтр происходит существенное уменьшение ширины его энергетического спектра (с DfX до DF) и, соответственно, увеличение времени корреляции (c tX до tY). В результате между некоррелированными отсчетами реакции фильтра Y(ktY) располагается примерно DfX /DF некоррелированных отсчетов воздействия X(ltX),, каждый из которых дает вклад в формирование единственного отсчета реакции с весом, определяемым видом импульсной характеристики фильтра.

Таким образом, в некоррелированных сечениях Y(ktY) происходит суммирование большого числа также некоррелированных случайных величин X(ltX) с ограниченными математическими ожиданиями и дисперсиями, что в соответствии с центральной предельной теоремой (А.М. Ляпунова) обеспечивает приближение распределения их суммы к нормальному с увеличением числа слагаемых.

5.3. Узкополосные случайные процессы

СП X(t) с относительно узким энергетическим спектром (DfX << fc) как и узкополосные детерминированные сигналы удобно представлять в квазигармонической форме (см. раздел 2.5)

,

где огибающая A(t), фаза Y(t) и начальная фаза j(t) являются случайными процессами, а ?с – частота, выбираемая произвольно (обычно как средняя частота его спектра).

Для определения огибающей A(t) и фазы Y(t) целесообразно воспользоваться аналитическим СП

.

Тогда

, (5.3)

, (5.4)

, (5.5)

. (5.6)

Основные моментные функции аналитического СП

:

1. Математическое ожидание

.

2. Дисперсия

.

3. Функция корреляции

,

при этом

.

Аналитический СП называют стационарным, если

,

откуда

.

Рассмотрим типичную в технике связи задачу прохождения нормального СП через полосовой фильтр (ПФ), амплитудный (АД) и фазовый (ФД) детекторы (рис. 5.7). Сигнал на выходе ПФ становится узкополосным

, а это означает, что его огибающая A(t) и начальная фаза j(t) будут медленно меняющимися функциями времени по сравнению с

, где

– средняя частота полосы пропускания ПФ. По определению, сигнал на выходе АД будет пропорционален огибающей входного сигнала A(t), а на выходе ФД – его начальной фазе j(t). Таким образом, для решения этой задачи достаточно вычислить распределение огибающей A(t) и фазы Y(t) (распределение начальной фазы

отличается от распределения Y(t) только математическим ожиданием

                                     X(t) = A(t)cosY( t)                            KАДА( t)

                     ПФ                                                   АД



                                                                                                KФДj( t)

                                                                              ФД



Рис. 5.7. Прохождение СП через полосовой фильтр и детекторы.

Постановка задачи

Дано:

1) X(t) = A(t)cosY(t) – узкополосный центрированный стационарный нормальный СП (на выходе ПФ),

2)

.

Определить:

1) w(A) – одномерную плотность вероятности огибающей,

2) w(Y) – одномерную плотность вероятности фазы.

Для решения этой задачи наметим три этапа:

1. Переход к аналитическому СП

и определение совместной плотности вероятности

.

2. Расчет совместной плотности вероятности

по вычисленной на первом этапе

и связям A(t), Y(t) с

(5.3) ÷ (5.6) .

3. Определение одномерных плотностей вероятности w(A) и w(Y) по вычисленной совместной плотности вероятности

.

Решение

1 этап. Найдем одномерную плотность вероятности

процесса

. На основе линейности преобразования Гильберта

делаем вывод о том, что

– нормальный СП. Далее, учитывая, что

, получаем

, а следовательно

.

Таким образом, имеем

.

Докажем некоррелированность

в совпадающие моменты времени, т. е. что

.

После подстановки

, учитывая, что при

, получим

.

Некоррелированность сечений нормальных процессов влечет их независимость, следовательно

.

2 этап. Расчет совместной плотности вероятности

,

где согласно (5.2), (5.5) и (5.6)

.

Следовательно, с учетом (5.3) имеем

. (5.7)

3 этап. Определение одномерных плотностей вероятности

Окончательно

, (5.8)

. (5.9)

Выражение (5.8) известно как распределение Рэлея, его график приведен на рис. 5.8. На рис. 5.9 приведен график равномерного распределения фазы (5.9).

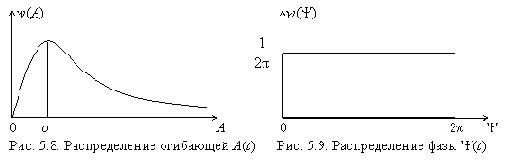
Выражение (5.7) можно представить в виде произведения (5.8) и (5.9)

,

из чего следует независимость огибающей A(t) и фазы w(Y) нормального СП.

Рассмотрим более сложную задачу прохождения аддитивной смеси выше рассмотренного нормального СП с гармоническим сигналом через АД и ФД. Постановка задачи сохраняется прежней за исключением исходного процесса Y(t) , который приобретает вид

,

где X(t) – центрированный нормальный СП.

Поскольку

,

то

.

Запишем Y(t) в квазигармонической форме

и будем решать задачу определения плотностей вероятности w(A) и w(j) по выше приведенному плану.

Предварительно запишем X(t) в квазигармонической форме и через его квадратурные компоненты

.

Тогда

,

где

Отсюда

, (5.10)

(5.11)

Для нахождения

обратимся к аналитическому СП

.

Из его выражения видно, что

являются линейными преобразованиями центрированного нормального СП X(t):

и, следовательно, имеют нормальное распределение с дисперсиями

.

Докажем их некоррелированность (а следовательно и независимость) в совпадающие моменты времени

.

Здесь учтено, что B(t) и ?(t) – огибающая и фаза нормального СП являются, как выше установлено, независимыми.

Таким образом,

и с учетом (5.10) и (5.11) получаем

. (5.12)

Поскольку выражение (5.12) невозможно представить в виде произведения одномерных функций

, то можно сделать вывод о зависимости процессов

.

Для нахождения распределения огибающей суммы центрированного нормального СП с гармоническим сигналом проинтегрируем (5.12) по всем возможным значениям случайной фазы j(t)

.

Интеграл вида

известен в математике как модифицированная функция Бесселя нулевого порядка. С его учетом окончательно имеем

. (5.13)

Выражение (5.13) называют обобщенным распределением Рэлея или распределением Райса. Графики этого выражения приведены на рис. 5.10 для следующих частных случаев:

1) U = 0

– обычное распределение Рэлея,

2)

– случай отсутствия в Y(t) СП X(t),

3)

– обобщенное распределение Рэлея (Райса).

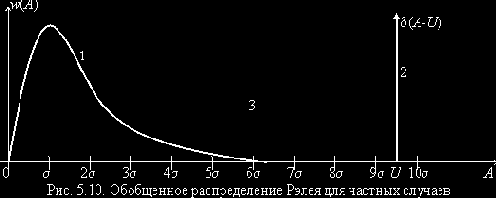
Из графиков видно, что чем больше отношение сигнал/шум

тем правее смещен максимум плотности вероятности и тем симметричнее (ближе к нормальному распределению) кривая

.

Выводы

1. Если мгновенные значения центрированного СП X(t) имеют нормальное распределение, то его огибающая A(t) распределена по закону Релея

,

а фаза Y(t) равномерно

.

2. Распределение огибающей аддитивной смеси центрированного нормального СП и гармонического сигнала подчиняется обобщенному распределению Рэлея (оно же распределение Райса)

.

Контрольные вопросы

1.     Сформулируйте задачу анализа прохождения СП через заданный функциональный узел.

2.     Как вычисляют плотность вероятности w(y) реакции безынерционной цепи по известной плотности вероятности w(x) воздействия?

3.     Как вычисляют математическое ожидание реакции безынерционной цепи на случайное воздействие X(t)?

4.     Как вычисляют дисперсию реакции безынерционной цепи на случайное воздействие X(t)?

5.     Как вычисляют функцию корреляции реакции безынерционной цепи на случайное воздействие X(t)?

6.     Как вычисляют совместную плотность вероятности w(у1, у2; t) двух СП Y1(t) и Y2(t), связанных известными функциональными зависимостями

с двумя другими СП X1(t) и X2(t)?

7.     Как меняется распределение нормального СП при его прохождении через линейную цепь?

8.     Как меняется произвольное распределение СП при его прохождении через узкополосный фильтр?

9.     В чем суть явления нормализации широкополосного процесса при его прохождении через узкополосный фильтр? Дайте математическое обоснование этому явлению.

10. Опишите процедуру корреляционного анализа прохождения СП через линейную цепь.

11. Дайте определение огибающей и фазы СП.

12. Дайте определения аналитическому СП, его математическому ожиданию, дисперсии и функции корреляции.

13. Каким условиям удовлетворяет стационарный аналитический СП?

14. Каково распределение огибающей центрированного нормального СП?

15. Каково распределение фазы центрированного нормального СП?

16. Каково распределение огибающей суммы центрированного нормального СП и гармонического сигнала?

17. Напишите аналитическое выражение закона Рэлея. Распределение какого СП он характеризует?

18. Напишите аналитическое выражение обобщенного закона Рэлея (закона Райса). Распределение какого СП он характеризует?

Рекомендации по проведению экспериментальных исследований

прохождения случайных процессов через различные ФУ

Для закрепления знаний, полученных при изучении данного раздела рекомендуется выполнить в рамках виртуальной лаборатории работу № 20 «Прохождение случайных процессов через различные функциональные узлы» в полном объеме (рис. 5.11).

Обратите внимание на характер распределения СП на выходах одностороннего и двустороннего ограничителей - реальное проявление d-функций в виде выбросов на гистограммах плотности вероятности распределения, соответствующих порогам ограничения. Убедитесь в нормализации СП с произвольными распределениями после их прохождения через ФНЧ и ПФ и в отсутствии нормализации после прохождения СП через ФВЧ (объясните почему?).

6. Оптимальный прием дискретных сообщений

6.1. Постановка задачи

Дано:

1. Источник дискретных сообщений. Это значит, что известен ансамбль передаваемых сообщений

, где m – объем алфавита источника

и их статистика (распределение вероятностей)

.

2.     Модулятор. Это значит, что известны правила преобразования каждого сообщения в непрерывный сигнал и длительность сигнала T

bi ® si(t); i = 1, 2,…, m;    t Î (0, T).

3.     Непрерывный канал. Канал задается своей математической моделью, описывающей связь его реакции Z(t) с воздействием si(t) и канальными помехами N(t), например

4. Тактовая синхронизация осуществляется идеально. Вопросы синхронизации не рассматриваются в рамках курса ТЭС, поэтому здесь и в дальнейшем всегда будем считать, что границы между сигналами si(t) в приемнике определяются точно, иначе говоря, в нем осуществляется дискретизация времени функцией d(t-kT), при которой границы тактов совпадают с границами сигналов.

Требуется:

Определить правило решения (решающую схему) вида

,

т.е. указать, каким образом на основе анализа принятой реализации z(t) СП Z(t) на каждом интервале Т следует принимать решение

о переданном символе bi (при j = i имеет место правильный прием, иначе (при j ? i) – ошибочный).

Дадим геометрическую трактовку этой постановке задачи (рис. 6.1). Совокупность всех возможных реализаций z(t) образует пространство принимаемых колебаний (обычно бесконечномерное пространство Гильберта L2(T)) в котором присутствуют m различных векторов

передаваемых сигналов si(t) (i = 1, 2,…, m). Выбор правила решения таким образом сводится к разбиению этого пространства на m непересекающихся областей

, каждая из которых соответствует принятию решения о передаче конкретного сообщения bi (сигналом si(t)). На рис. 6.1. показаны две ситуации: 1) конец вектора колебания

попадает в область

отведенную под решение о передаче сообщения bk сигналом sk(t), что соответствует правильному приему; 2) конец вектора колебания

попадает в область

, отведенную под решение о передаче сообщения bj сигналом sj(t), что соответствует ошибочному приему.

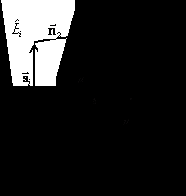
Разные правила решения (разные приемные устройства) различаются способом разбиения пространства принимаемых колебаний на области

. В этой связи возникает задача наилучшего разбиения, которое, очевидно, всегда существует в определенном смысле. Например, если сообщение bi передается чаще сообщения bj и важно , чтобы как можно меньше передаваемых символов принимались ошибочно, то следует область

расширить за счет области

. Наилучшее разбиение пространства принимаемых сигналов (оптимизация решающей схемы) может быть найдено на основе критерия качества приема, разработка которого требует отдельного рассмотрения на основе теории статистический решений.

В такой постановке задача приема дискретных сообщений в канале с аддитивной, нормальной помехой была решена В.А. Котельниковым (1946 г.), заложившим основы теории потенциальной помехоустойчивости.

Приемник, реализующий наилучшее разбиение пространства принимаемых сигналов по выбранному критерию качества приема, Котельников назвал идеальным, а достигаемую им помехоустойчивость, при которой обеспечивается максимум средней вероятности правильного приема при заданной модуляции, – потенциальной помехоустойчивостью. Мы будем в дальнейшем такой идеальный приемник называть оптимальным демодулятором, как это часто принято в современной теории связи.

Теория потенциальной помехоустойчивости конструктивна, т.к. позволяет не только определить пределы достигаемой помехоустойчивости, но и указывает пути реализации соответствующих демодуляторов.

6.2. Критерии качества приема дискретных сообщений

6.2.1. Критерий идеального наблюдателя

(критерий Котельникова)

Этот критерий требует обеспечения минимума средней вероятности ошибочного приема.

Для двоичной системы

,

для m-ичной системы

,

где

– условная вероятность j-ой ошибки при передаче

i-го сообщения,

– условная вероятность любой ошибки при передаче

i-го сообщения,

Р – безусловная вероятность любой ошибки.

Вычислим условную вероятность конкретной ошибки

,

где

– n-мерная условная плотность вероятности (при разложении

в n-мерном евклидовом пространстве по любому базису), а интеграл, вычисляемый по векторной переменной

, очевидно, n-кратный. Таким образом, критерий Котельникова приобретает вид

, (6.1)

где

находится варьированием областей

.

Минимуму средней вероятности ошибок соответствует максимум средней вероятности правильного приема (иная эквивалентная форма записи критерия Котельникова)

. (6.2)

Учитывая, что демодулятор должен реализовать критерий (6.1) или (6.2), принимая решение

на основе анализа единственной реализации
на интервале 0 – Т, рассмотрим апостериорную вероятность вида

, т.е. вероятность того, что при приеме сигнала

передавалось сообщение bi .

Очевидно, что максимум средней вероятности правильного приема будет достигнут, если всякую реализацию принятого колебания z(t) относить к той области

, для которой апостериорная вероятность

максимальна, т.е. решение в пользу

принимается при совместном выполнении совокупности неравенств

.

Иначе говоря, критерий Котельникова требует максимизации апостериорной (обратной) вероятности и его можно записать в виде

. (6.3)

Для выполнения анализа (6.3) воспользуемся известной формулой Байеса

.

Тогда

,

а выражение (6.3) принимает вид

(6.4)

(безусловная плотность вероятности

здесь исключена, т. к. она не зависит от i и, следовательно, не влияет на решение).

В развернутом виде критерий (6.4) можно записать в виде системы из m-1 неравенств

,

или

.

Условную плотность вероятности

, рассматриваемую при известном после приема векторе

как функцию аргумента bi, называют функцией правдоподобия гипотезы о передаче сообщения bi, а

- отношением правдоподобия двух гипотез о передаче сообщений bi и bj. С учетом этого критерий Котельникова можно записать в виде:

если

, то решение

. (6.5)

Рассмотренный критерий Котельникова обладает следующими особенностями:

1) требует знания априорных безусловных вероятностей отдельных сообщений

;

2) безразличен к виду ошибок

(все виды ошибок одинаково нежелательны), что приводит к росту ошибок при приеме менее вероятных сообщений, а они являются более информативными.

6.2.2. Критерий максимального правдоподобия

Полагая, что все передаваемые сообщения равновероятны

,

из (6.5) получим

если

, то решение

.

Удобно помимо гипотез о передаче сообщений bi (i = 1, 2,…, m) ввести еще одну «нулевую» гипотезу о том, что никакое сообщение (сигнал) не передавалось, т. е. принятое колебание является реализацией только помехи

. Обозначим отношение правдоподобия

,

тогда правило решения можно записать в виде

если

, при всех

, то решение

или

. (6.6)

Критерий (6.6) называют критерием максимального правдоподобия. Он совпадает с критерием Котельникова при равных вероятностях передаваемых сообщений.

6.2.3. Критерий минимального среднего риска

(байесовский критерий)

Для учета разных последствий ошибок передачи различных сообщений следует обобщить критерий Котельникова, минимизируя сумму условных вероятностей

в его выражении (6.1) с заранее назначенными весами (ценой, платой) Li,j. Средневзвешенная сумма условных вероятностей

при передаче сообщения bi (обычно называемая условным риском) имеет вид

,

а сам критерий требует

,                          (6.7)

где R – средний риск.

При использовании этого критерия оптимальной считается решающая схема, обеспечивающая наименьшее значение среднего риска (6.7).

Из критерия минимального среднего риска, как наиболее общего, вытекают оба вышерассмотренных критерия:

1)    критерий Котельникова при Li,i = 0 и Li,j = const (i ? j ),

2)    критерий максимального правдоподобия при Li,i = 0 и

.

Практическое использование критерия минимального среднего риска затруднено необходимостью знать вероятности передачи сообщений

и сложностью объективного определения весовых коэффициентов Li,j.

6.2.4. Критерий Неймана-Пирсона

Критерий Неймана-Пирсона применяется в двоичных системах в ситуациях, когда невозможно определить априорные вероятности отдельных сообщений, а последствия ошибок разного рода неодинаковы. Такая ситуация типична для радиолокации, где осуществляется зондирование пространства узким радиолучом и прием отраженного от цели сигнала. При этом имеют место две ситуации: 1) наличие цели – колебание на входе приемника содержит сигнал в аддитивной смеси с помехой (с неизвестной априорной вероятностью P(b1)), 2) отсутствие цели – на входе приемника действует одна помеха (с вероятностью P(b0) = 1 – P(b1)). Задача приема – обнаружение сигнала на фоне помех.

При ее реализации возможны два вида ошибок:

1) пропуск цели (цель есть, но отраженный сигнал не обнаружен) с условной вероятностью

;

2) ложная тревога (цель отсутствует, но принято решение о наличии отраженного сигнала) с условной вероятностью

.

Очевидно, что последствия этих ошибок сильно различаются.

В таком случае целесообразно стремиться к уменьшению условной вероятности ошибки, вызывающей особо тяжелые последствия (пропуск цели), что можно сделать только за счет увеличения вероятности ошибки другого вида (ложной тревоги). Ясно, что это можно делать до определенной степени, т. к. слишком большая вероятность ложной тревоги приведет к ощутимым экономическим потерям и к подрыву доверия к системе в целом. Разумный выход – зафиксировать вероятность ложной тревоги на выбранном уровне ?

, (6.8)

и затем минимизировать вероятность пропуска цели

. (6.9)

Минимизация (6.9) при заданной величине (6.8) достигается, если решение о наличии цели принимается при выполнении неравенства

,

где ?(?) – пороговый уровень, определяемый заданной вероятностью ложной тревоги.

Контрольные вопросы

1.     Сформулируйте задачу оптимального приема дискретных сообщений.

2.     Дайте геометрическую трактовку задаче оптимального приема дискретных сообщений.

3.     Что называют правилом решения (решающей схемой) демодулятора?

4.     Что такое идеальный (оптимальный) приемник дискретных сообщений?

5.     Что понимают под потенциальной помехоустойчивостью приема дискретных сообщений?

6.     В чем суть теории потенциальной помехоустойчивости? Когда и кем были заложены ее основы?

7.     Какой смысл вкладывают в понятие критерия качества приема дискретных сообщений? Перечислите известные Вам критерии.

8.     В чем суть критерия идеального наблюдателя (критерия Котельникова)?

9.     Укажите особенности критерия Котельникова.

10. Что представляет собой критерий максимального правдоподобия? Как он соотносится с критерием Котельникова?

11. Расскажите о критерии минимального среднего риска. В чем его общность?

12. При каких условиях критерий минимального среднего риска совпадает с критерием Котельникова?

13. При каких условиях критерий минимального среднего риска совпадает с критерием максимального правдоподобия?

14. В чем сущность критерия Неймана-Пирсона? В каких случаях целесообразно его использование?

6.3. Синтез оптимального демодулятора при

известном ансамбле сигналов (когерентный прием)

6.3.1. Постановка и решение задачи когерентного приема

          на корреляторах

Постановка задачи:

Известны:

1.     Ансамбль сигналов на выходе модулятора

{si(t)}; i = 1, 2,…, m;    t Î (0, T).

2.     Непрерывный канал

,

где N(t) – квазибелый нормальный шум, т. е.

.

3. В качестве критерия качества приема задан критерий максимального правдоподобия (6.6)

Требуется синтезировать оптимальный демодулятор, иначе говоря, найти алгоритм оптимальной обработки входного сигнала и принятия решения о передаваемом сообщении.

Решение

В основу решения положим выражение заданного критерия качества приема, для чего рассмотрим входящие в него функции правдоподобия гипотез:

1) о наличии во входном колебании z(t) i-го сигнала [z(t) = si(t) + n(t)]

,

2) об отсутствии в нем какого-либо сигнала [z(t) = n(t)]

,

где

.

Начнем с последней. Учитывая, что сечения квазибелого шума, разделенные интервалами

, не коррелированны, а в силу нормального распределения шума и независимы, получим

.

Поскольку СП Z(t) = si(t)+ N(t) отличается от шума N(t) только известным, а потому неслучайным сигналом si(t), играющим роль математического ожидания Z(t), то

,

где использовано обозначение si,k = si(tk).

В итоге отношение правдоподобия гипотез о наличии и отсутствии сигнала принимает вид

или с учетом

.

Перейдем к белому шуму, сняв ограничение на ширину его спектра (F ® ¥). Иначе говоря, от евклидова пространства перейдем к гильбертовому. При этом

. (6.10)

Синтезируемый демодулятор должен принимать решение в пользу

, обеспечивающего максимум выражения (6.10), или, что эквивалентно, максимум показателя экспоненты в нем

. (6.11)

Нетрудно видеть, что максимум (6.11) достигается при минимуме вычитаемого

. (6.12)

Демодулятор оптимальный по критерию максимального правдоподобия принимает решение в пользу того символа

, сигнал si(t) которого отстоит от принятого колебания z(t) на меньшее расстояние.

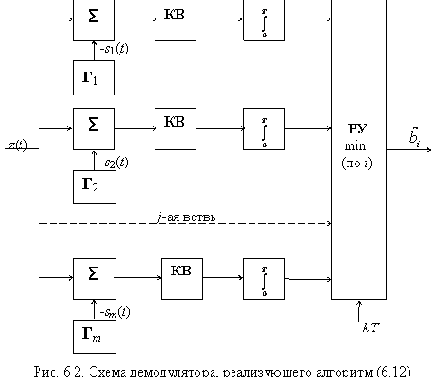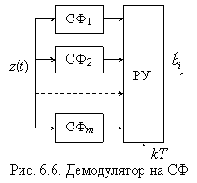
Рассматривая выражение (6.12) как алгоритм обработки принятого колебания z(t) приходим к схеме демодулятора, представленной на рис. 6.2.

Другую форму алгоритма можно получить из выражения (6.11)

,

или

, (6.13)

где Ei – энергия i-го сигнала.

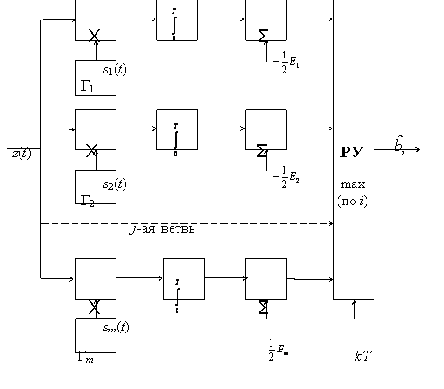Схема оптимального демодулятора, реализующего алгоритм (6.13), приведена на рис. 6.3. Поскольку в каждой ветви такого демодулятора присутствует вычислитель скалярного произведения

– коррелятор, то его называют демодулятором на корреляторах (активных фильтрах).

Если использовать сигналы равных энергий, то алгоритм (6.13) и схема демодулятора (рис. 6.3) существенно упрощаются (рис. 6.4)

. (6.14)

Все вышерассмотренные демодуляторы используют всю информацию о форме сигналов si(t), включая начальную фазу. В каждой их ветви содержатся генераторы, генерирующие синфазные образцы этих сигналов, поэтому их называют когерентными демодуляторами.

6.3.2. Синтез оптимального когерентного демодулятора

на согласованных фильтрах

Сохраняя постановку задачи синтеза демодулятора из предыдущего раздела и опираясь на алгоритмы (6.13) и (6.14), попробуем заменить коррелятор (активный фильтр), вычисляющий скалярные произведения приходящего колебания и образцов сигналов, на пассивный линейный фильтр, реализующий ту же операцию.

Как известно, реакция линейного фильтра на воздействие z(t) вычисляется с помощью интеграла Дюамеля

Потребуем, чтобы в заранее выбранный момент времени t0 значение этой реакции y(t0) с точностью до коэффициента совпало со скалярным произведением (6.14)

.

Как видно, это достигается при

и t0 ? T . После замены переменных

получаем

. (6.15)

Фильтры, обладающие такими импульсными характеристиками, называют согласованными (СФ) с соответствующими сигналами.

На рис. 6.5 изображены сигнал длительностью Т и импульсные характеристики согласованных с ним фильтров для t0 = Т и t0 > Т, из которых видно, что импульсная характеристика согласованного фильтра является «зеркальным отражением» сигнала относительно момента времени 0,5t0.

Таким образом, фильтры с импульсными характеристиками (6.15) вполне могут заменить корреляторы в ветвях оптимального демодулятора (рис. 6.3 и 6.4), если решения принимать по отсчетам их реакции yi(kT) (рис. 6.6).

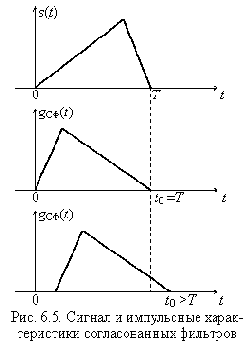
Свойства согласованных фильтров

1. Импульсная характеристика СФ является «зеркальным отражением» сигнала, с которым он согласован, относительно момента времени 0,5t0 (с точностью до постоянного коэффициента)

.

Это свойство было положено в основу определения СФ (6.15).

2. Передаточная функция СФ

.

После замены t0 – t = t, t = t0 – t, dt = –dt, при t ® ¥ t ® -¥

.

Таким образом, передаточная функция СФ с точностью до множителя

совпадает с сопряженной спектральной функцией сигнала, с которым он согласован

.

Амплитудно-частотная характеристика СФ

с точностью до коэффициента а повторяет амплитудный спектр сигнала, с которым он согласован

Фазо-частотная характеристика СФ

отличается знаком от фазового спектра сигнала, с которым он согласован (без учета слагаемого –?t0).

3. Форма отклика СФ на «свой» сигнал (сигнал с которым он согласован)

.

Учитывая, что из (6.15) вытекает

, получим

.

Таким образом, отклик СФ на «свой» сигнал с точностью до коэффициента совпадает с его корреляционной функцией, смещенной по оси времени на интервал t0 (рис. 6.7)

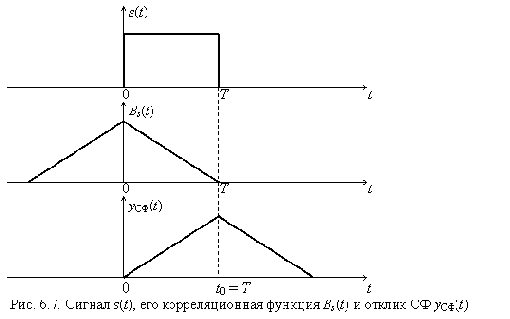
Из полученного результата вытекают следующие выводы:

Отклик СФ на «свой» сигнал с точностью до постоянного коэффициента совпадает с его корреляционной функцией.
Длительность отклика на «свой» сигнал всегда равна 2Т.
СФ не восстанавливает форму сигнала, искаженного шумом. Его задача создать один отсчет y(t0), по которому можно наилучшим образом судить о присутствии на входе «своего» сигнала.

4. СФ обеспечивает наибольшее отношение сигнал/шум (с/ш) на своем выходе при действии на входе аддитивной смеси «своего» сигнала и центрированного нормального белого шума

со спектральной плотностью мощности N=NО/2.

Докажем это, уточнив предварительно, что под отношением с/ш на выходе СФ понимают отношение математического ожидания отсчета случайной реакции СФ Y(t) в момент времени t0 = T к корню из ее дисперсии

. (6.16)

Рассмотрим произвольный линейный фильтр с передаточной функцией

. Поскольку

представляет собой отсчет реакции ys(T) на математическое ожидание воздействия, каковым является сигнал s(t), то

.

Полученное выражение представляет собой не что иное, как скалярное произведение

двух векторов

в комплексном пространстве Гильберта, если иметь в виду следующие соответствия:

.

Вычислим дисперсию случайной величины

Подставляя полученные результаты в выражение (6.16) и применяя неравенство Коши-Буняковского-Шварца

,

имеем

.

Наибольшее значение с/ш (равенство в полученном выражении) достигается при совпадении векторов

, т. е. для случая использования СФ, что и требовалось доказать. Это чрезвычайно важное свойство некоторые авторы закладывают в основу определения СФ.

Найдем саму величину отношения с/ш на выходе СФ при действии на его входе «своего» сигнала

,                 (6.17)

где Е – энергия «своего» сигнала,

       NО – односторонняя спектральная плотность мощности шума,

.

Таким образом, максимальное отношение с/ш на выходе СФ определяется энергией «своего» сигнала, независимо от его формы.

Определим отношение с/ш по мощности

,

где FK – ширина полосы пропускания канала.

При совпадении ширины полосы пропускания канала с шириной спектра сигнала FK = Fs имеем

.

Отсюда вытекает целесообразность выбора сигналов с большой базой 2FsT для передачи дискретных сообщений, что позволяет увеличить отношение с/ш при согласованной фильтрации.

6.3.3. Согласованная фильтрация и корреляционный прием

некоторых типичных сигналов

Рассмотрим особенности когерентного приема некоторых сигналов и реализации соответствующих согласованных фильтров.

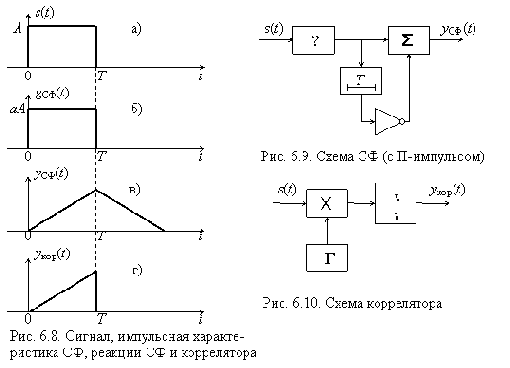
Прямоугольные видеоимпульсы

Сигнал в виде прямоугольного видеоимпульса s(t) (рис. 6.8,а) и импульсная характеристика gСФ(t) согласованного с ним фильтра (рис. 6.8,б) описываются выражениями

Вычислим передаточную функцию СФ

.

Сомножитель

представляет собой передаточную функцию интегратора, вычитаемое

в скобках

– передаточная функция элемента задержки на время Т, а сама скобка соответствует алгебраическому сумматору. В итоге приходим к схеме СФ, показанной на рис. 6.9.

Реакция СФ на прямоугольный импульс показана на рис. 6.8,в. Для сравнения на рис. 6.8,г показана реакция на тот же сигнал коррелятора (рис. 6.10).

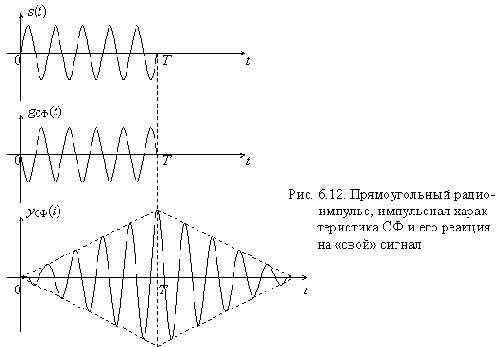
Прямоугольные радиоимпульсы

Сигнал в виде прямоугольного радиоимпульса s(t) описывается выражением

Импульсная характеристика gСФ(t) согласованного с ним фильтра на интервале

.

Такого рода импульсной характеристикой обладает колебательный контур с добротностью Q ® ¥, однако, у него она продолжается во времени неограниченно. Для «гашения» импульсной характеристики (реакции контура на воздействие d(t)) в момент t=T можно воспользоваться соответствующей коммутацией контура (рис. 6.11,а) или вычитанием самой задержанной на T реакции (рис. 6.11,б).

Прямоугольные радиоимпульсы и реакции на них СФ и коррелятора можно видеть на рис. 6.12, 6.19, 6.20 и 6.21.

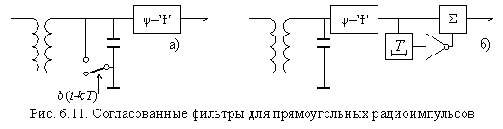
Сложные двоичные сигналы

Рассмотрим сигналы в виде n-последовательностей импульсов прямоугольной формы положительной и отрицательной полярности с фиксированным размахом.

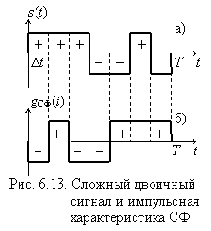
Возможный вид такого сигнала при n = 7 показан на рис. 6.13,а. Усложнение сигнала объясняется желанием получить определенную (острую) форму отклика на выходе согласованного с ним фильтра и повысить отношение с/ш. Поскольку

, то ясно – чем острее (короче)

, тем шире спектр сигнала и больше его база. Сигналы такого рода удобно использовать в радиолокационных и в асинхронно адресных телекоммуникационных системах.

Синтез СФ для сложного двоичного сигнала произведем, отталкиваясь от его импульсной характеристики (рис. 6.13,б). Видно, что требуемую форму

можно получить суммированием прямоугольных импульсов длительностью

, сдвинутых на кратные

интервалы времени, с соответствующими полярностями. Такие импульсы можно получить «размножением» единственного исходного П-импульса длительностью

с помощью линии задержки (ЛЗ) с n отводами (через

), а сам П-импульс в качестве импульсной характеристики – на выходе фильтра (СФП), согласованного с ним по форме. Эти рассуждения приводят нас к схеме фильтра, называемого трансверсальным (ТФ) (рис. 6.14). В цепях отводов ЛЗ включены повторители или инверторы сигналов с коэффициентами передачи +1 или -1 соответственно.

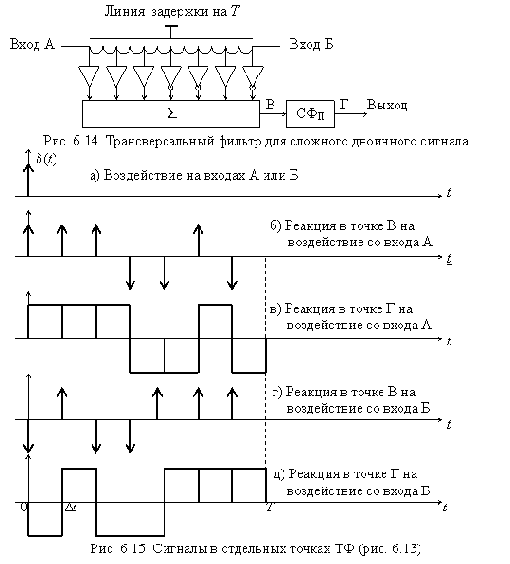
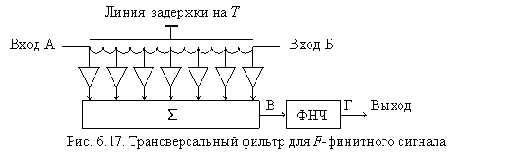
Проанализируем импульсную характеристику ТФ со стороны входа А, как его реакцию на воздействие в виде d-функции. Поданная этот вход d-функция (рис. 6.15,а) появится на отводах ЛЗ с соответствующими задержками и после суммирования в сумматоре (с учетом полярности) создаст последовательность, показанную на рис. 6.15,б. На выходе СФП, согласованного с одиночным П-импульсом длительностью

, каждая из этих d-функций вызовет реакцию (по определению – импульсную характеристику) в виде самого этого импульса. В результате получим на выходе ТФ n-последовательность, изображенную на рис. 6.15,в, т.е. рассмотренная схема работает как формирователь сложного двоичного сигнала (рис.6.14,а). Интересно, что при подаче d-функции на вход Б на выходе ТФ получим реакцию (смотри графики на рис. 6.15,г и 6.15,д), совпадающую с показанной на рис. 6.13,б.

Таким образом, один и тот же ТФ можно использовать в качестве формирователя сложного двоичного сигнала (вход А) и в качестве согласованного с этим сигналом фильтра (вход Б).

Из двоичных n-последовательностей наибольший интерес представляют собой последовательности (коды) Баркера. Они обладают важным свойством

,

где ВБОК – величина боковых лепестков корреляционной функции,

В(0) – начальное значение корреляционной функции.

Показанная на рис. 6.14 двоичная последовательность как раз и является кодом Баркера при n = 7. Импульсную характеристику и реакцию фильтра, согласованного с семиэлементным кодом Баркера, на этот «свой» сигнал (смещенную на Т корреляционную функцию кода Баркера) можно видеть на рис. 6.22.

Произвольные F-финитные сигналы

Согласно теореме Котельникова сигналы с ограниченным частотой F спектром точно передаются последовательностью своих отсчетов, взятых через интервалы

и, следовательно, могут быть заменены ступенчатой функцией (рис. 6.16,а), которая отличается от двоичного сигнала (рис. 6.13,а) только размахами отдельных П-импульсов длительностью

. Отсюда вытекает возможность формирования такого рода сигналов и их согласованной фильтрации с помощью аналогового трансверсального фильтра (рис. 6.17, 6.24). Его схема отличается от схемы двоичного ТФ (рис. 6.14) только заменой фильтра, согласованного с П-ипульсом (СФП) на сглаживающий фильтр (ФНЧ с частотой верхнего среза F) и использованием в цепях отводов ЛЗ усилителей с коэффициентами усиления, пропорциональным отсчетам F-финитного сигнала.

6.3.4. Оптимальный когерентный прием при небелом шуме

Рассмотрим задачу синтеза согласованного фильтра, обеспечивающего максимальное отношение с/ш на своем выходе для случая, когда на его входе действует аддитивная смесь известного сигнала s(t) и нормального небелого (окрашенного) шума (G(w) ? N = const). Эту задачу можно решить, разделив синтезируемый фильтр на два последовательно включенных (рис. 6.18). От первого из них потребуем выравнивания энергетического спектра шума, т.е.

превращения его в белый. По этой причине этот фильтр называют обеляющим. Его передаточную функцию Н1(w) можно определить из условия

Передаточную функцию второго фильтра определим из условия его согласования с сигналом s1(t). Для этого предварительно найдем его спектральную функцию

.

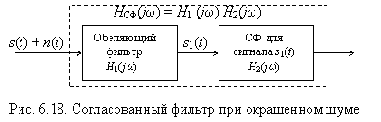
Тогда

Теперь можно вычислить передаточную функцию искомого СФ

.

Аналогично поступают при реализации оптимального когерентного демодулятора на корреляторах.

Контрольные вопросы

1.        Сформулируйте задачу синтеза оптимального когерентного демодулятора.

2.        Выведите алгоритм работы оптимального когерентного демодулятора.

3.        Нарисуйте схему оптимального когерентного демодулятора на корреляторах.

4.        В чем проявляется упрощение алгоритма (схемы) оптимального когерентного демодулятора при выборе ансамбля сигналов с равными энергиями?

5.        Какие фильтры называют согласованными с сигналами?

6.        Как импульсная характеристика согласованного фильтра связана с сигналом, с которым фильтр согласован?

7.        Каковы передаточная функция, АЧХ и ФЧХ согласованного фильтра?

8.        Какова форма отклика согласованного фильтра на «свой» сигнал?

9.        Какова длительность отклика согласованного фильтра на «свой» сигнал?

10.    Чему равно отношение с/ш на выходе согласованного фильтра?

11.    В какой степени изменяется отношение с/ш при согласованной фильтрации аддитивной смеси сигнала с нормальным белым шумом?

12.    Нарисуйте схему оптимального когерентного демодулятора на согласованных фильтрах.

13.    Нарисуйте схему реализации согласованного фильтра для прямоугольного видеоимпульса.

14.    Нарисуйте импульсную характеристику фильтра, согласованного с прямоугольным видеоимпульсом, и его реакцию на «свой» сигнал.

15.    Нарисуйте схему реализации согласованного фильтра для прямоугольного радиоимпульса.

16.    Нарисуйте импульсную характеристику фильтра, согласованного с прямоугольным радиоимпульсом, и его реакцию на «свой» сигнал.

17.    Нарисуйте импульсную характеристику фильтра, согласованного со сложным двоичным сигналом, и его реакцию на «свой» сигнал.

18.    Какие двоичные n-последовательности относятся к кодам Баркера? Каким свойством обладают их корреляционные функции? В чем полезность этих свойств для связи и радиолокации?

19.    Нарисуйте схему трансверсального фильтра для формирования и согласованной фильтрации сложного двоичного сигнала.

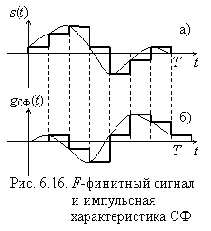
20.    Нарисуйте схему трансверсального фильтра для формирования и согласованной фильтрации произвольного F-финитного сигнала.

21.    Какова передаточная функция, АЧХ и ФЧХ согласованного фильтра при небелом шуме на его входе?

Рекомендации по проведению экспериментальных исследований

оптимального когерентного приема

Для закрепления знаний, полученных при изучении разделов 6.1-6.3, целесообразно выполнить лабораторные работы № 15 «Исследование когерентных демодуляторов» (рис. 6.19, 6.20) и № 22 «Согласованная фильтрация сигналов известной формы» (рис. 6.21 – 6.24) в полных объемах, а также дополнительные экспериментальные исследования в рамках предоставляемых этими работами ресурсов. Обратите внимание на общее и различное в реакциях корреляторов и согласованных фильтров на «свои» и «чужие» сигналы, на связи с АЧХ СФ с амплитудными спектрами «своих» сигналов.

При исследовании согласованных фильтров убедитесь в соответствии их импульсных характеристик, АЧХ и реакций на «свои» сигналы теоретическим результатам, полученным выше. Убедитесь также, что отсчет реакции СФ на «свой» сигнал в момент времени t0 = T всегда больше отсчета на любой «чужой» сигнал.

Обратите также внимание на минимальный уровень боковых лепестков корреляционной функции кода Баркера по сравнению с любыми иными двоичными последовательностями той же длины (рис. 6.23).

Убедитесь в широких возможностях формирования F-финитных сигналов различных форм с помощью трансверсального фильтра и согласованной фильтрации такого рода сигналов (рис. 6.24).

6.4. Потенциальная помехоустойчивость когерентного приема

Постановка задачи:

Известны:

1.     Ансамбль сигналов на выходе модулятора

{si(t)}m; i = 1, 2,…, m;    t Î (0, T).

2.     Непрерывный канал

,

где N(t) – квазибелый нормальный шум, т. е.

.

3. Алгоритм работы демодулятора (оптимального когерентного по критерию максимального правдоподобия) (6.13)

.

Определить Р - среднюю вероятность ошибочного приема.

Ограничимся случаем двоичной системы (m = 2), когда

.

Перепишем алгоритм (6.13) в развернутом виде

,

или

.

Из иной записи того же алгоритма

вытекает достаточность одной ветви в оптимальном демодуляторе, которая должна содержать либо коррелятор с опорным генератором разностного сигнала, либо согласованный с этим разностным сигналом фильтр (рис. 6.25). В этих демодуляторах в качестве решающих устройств используются компараторы со стробированием. Компаратор представляет собой дифференциальный усилитель с цифровым выходом и коэффициентом усиления К ® ¥. Напряжение на выходе компаратора может принимать одно из двух значений: высокое (уровень логической «1»), если напряжение на его прямом входе больше, чем на инверсном, и низкое (уровень логического «0») в противном случае. В данном случае производится сравнение выходного напряжения коррелятора или СФ с пороговым в моменты kT поступления коротких стробирующих импульсов.

Символом «= =» в УГО компаратора обозначена операция сравнения, а кружком – инверсный вход.

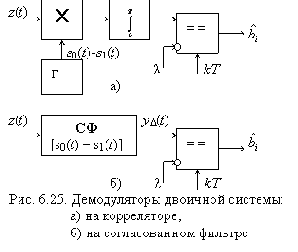
Для решения поставленной задачи рассмотрим случайную величину YD(T) – отсчеты реакции СФ в конце каждого сигнала на входной СП Z(t) = si(t) + N(t).

Очевидно, что YD(T) имеет нормальное распределение с двумя возможными математическими ожиданиями

:

y0 – при передаче сообщения b0,

y1 – при передаче сообщения b1.

.

Условные распределения величины YD(T) показаны на рис. 6.26

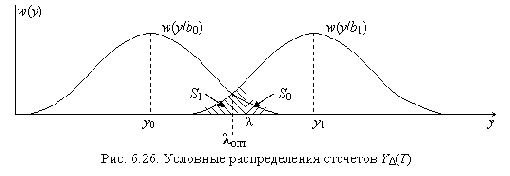
В двоичных системах имеют место ошибки двух типов. Определим их вероятности

.

Средняя вероятность ошибочного приема

.

При равных вероятностях передаваемых сообщений

.

Минимизация Р означает минимизацию суммы S0 + S1, что достигается при выборе оптимального порога ?опт, определяемого из условия

(рис. 6.26)

.

При таком выборе порога

и, следовательно, для вычисления средней вероятности ошибочного приема Р достаточно определить любую условную вероятность ошибок, например,

.

Произведя замену переменных

,

получим

,                   (6.18)

где Q(?опт) – дополнительная функция ошибок,

      F(?опт) – функция ошибок,

      Ф(?опт) – функция Крампа.

Все эти функции табулированы, их можно найти в математических справочниках.

Полученный результат свидетельствует, что для любой двоичной системы при когерентном приеме вероятность ошибок определяется исключительно величиной ?опт, на которой сосредоточим свое внимание. Из рассмотренного вытекает

,

где

– математическое ожидание отклика фильтра, согла-

                   сованного с разностным сигналом sЭ(t) = s1(t) – s0(t),

                   на   «свой» сигнал в момент t = T,

       ? – квадратный корень из дисперсии этого отклика.

Используя ранее вычисленное значение отношения с/ш на выходе согласованного фильтра (6.17), получаем

,                          (6.18)

где ЕЭ – энергия разностного (эквивалентного) сигнала sэ(t),

      NO – спектральная плотность мощности шума,

.

Учитывая геометрический смысл энергии сигнала

, выражение (6.18) можно переписать в виде

.

Выводы

1. Помехоустойчивость когерентного приема в двоичных системах определяется исключительно соотношением энергии ЕЭ разностного сигнала (расстоянием между сигналами) и спектральной плотности мощности NO нормального белого шума

. (6.19)

2. Средняя вероятность ошибочного приема для этого случая вычисляется с помощью дополнительной функции ошибок по формуле

(6.20)

6.5. Сравнительный анализ потенциальной

помехоустойчивости основных видов цифровой модуляции

Для сравнения помехоустойчивости основных видов цифровой модуляции АМ, ЧМ (при использовании ортогональных сигналов) и ФМ достаточно для каждого из них определить эквивалентную энергию ЕЭ разностного сигнала sэ(t) = s1(t) – s0(t) или расстояние между этими сигналами и воспользоваться выражением (6.20). Сравнение удобно выполнять на энергетической основе, т.е. определять соотношение энергий сигналов с разными видами модуляции, при котором обеспечиваются равные вероятности ошибочного приема. На рис. 6.27. в двумерном пространстве показаны векторы сигналов s0(t), s1(t) с равными энергиями и sэ(t) для: а) АМ (при s0(t) = 0), б) ЧМ и в) ФМ.

Из этих рисунков и (6.20) следует:

(6.21)

(6.22)

(6.23)

где

Для достижения одинаковой помехоустойчивости (РАМ = РЧМ = РФМ) энергия сигналов Е при ЧМ должна быть в 2 раза, а при ФМ – в 4 раза меньше чем при АМ, т.е. по пиковой мощности ЧМ обеспечивает двукратный, а ФМ четырехкратный энергетический выигрыш по сравнению с АМ. По средней мощности выигрыши ЧМ и ФМ уменьшаются в 2 раза за счет пассивной паузы при АМ.

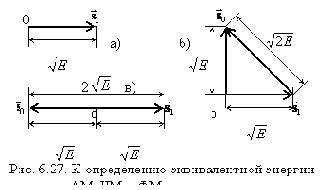
Таким образом, при равных энергиях сигналов наибольшей помехоустойчивостью обладает система с ФМ (использующая противоположные сигналы), наименьшей – система с АМ (с пассивной паузой). Система с ЧМ, использующая ортогональные сигналы, занимает промежуточное положение.

Следует отметить, что оптимальный порог в демодуляторе при использовании АМ не равен нулю, как при ЧМ и ФМ (при использовании сигналов с равными энергиями). Он зависит от энергии Е (мощности) сигнала, которая может быть неизвестной или изменяться в процессе передачи, что затрудняет практическую реализацию оптимального приема.

Полученные результаты имеют общий характер и относятся не столько к конкретному виду модуляции при использовании гармонического переносчика, сколько к выбору сигналов. В частности, формулы расчета средней вероятности ошибочного приема применимы для любых двоичных систем:

(6.21) - с пассивной паузой,

(6.22) – с ортогональными сигналами,

(6.23) – с противоположными сигналами.

Практическая реализация оптимального приема сигналов с наиболее помехоустойчивой модуляцией – ФМ является весьма проблематичной из-за чрезмерных требований к точности работы системы синхронизации:

1. При использовании согласованной фильтрации требуется высокая временная точность взятия отсчета реакции на выходе СФ (погрешность не должна превышать малой доли периода несущей частоты).

2. При использовании активного фильтра (коррелятора) столь же высокие требования предъявляются к фазовой погрешности опорного колебания.

Использование автономного опорного генератора в демодуляторе по этой причине исключается. Использование систем автоподстройки его частоты и фазы к соответствующим параметрам несущего колебания невозможно по причине отсутствия оного в спектре ФМ сигнала (при равновероятных сообщениях). Возможный выход из этой ситуации состоит в использовании различных схем восстановления несущего колебания из принимаемого сигнала, например, схемы Пистолькорса А.А., использующей последовательно включенные умножитель и делитель частоты в два раза (рис. 6.28). Однако, все схемы такого рода обладают существенным недостатком – неоднозначностью фазы (0 или ?) восстановленного колебания несущей частоты, что может приводить к так называемой «обратной работе», когда принимаемые сообщения инвертируются, т.е. вместо 0 регистрируются 1 и наоборот.

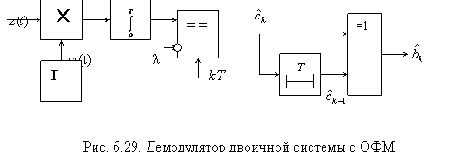
Эффективный способ решения этих проблем был предложен Н.Т.Петровичем путем перехода к относительной фазовой модуляции (ОФМ). При ОФМ сообщение («0» или «1») передается не абсолютным значением фазы несущего колебания (0 или ?), а разностью фаз текущего и предшествующего сигналов, т.е.

«0» передается сохранением фазы колебания, а «1» ее изменением на ?. Систему с ОФМ можно рассматривать как систему с ФМ со специальным перекодированием кодовых символов bk в ck на входе фазового модулятора по правилу ck = bk Å ck-1. Символ Å означает суммирование по модулю 2 (логическую операцию «исключающее ИЛИ»). Принимать сигналы с ОФМ можно с помощью фазовых демодуляторов (рис. 6. 18) с последующим обратным перекодированием выходных символов (рис. 6.29). В этой схеме обратное перекодирование осуществляется логическим элементом «исключающее ИЛИ» (символ «=1» на УГО) совместно с элементом задержки на Т.

Определим вероятность ошибочного приема в системе с ОФМ при когерентном приеме. Поскольку в формировании выходного символа

участвуют символы

, ошибочный прием имеет место при выполнении одного из двух условий:

1. символ

принят верно, а символ

ошибочно,

2. символ

принят ошибочно, а символ

верно.

Каждое из этих условий реализуется с вероятностью РФМ(1-РФМ). Таким образом получаем

. Поскольку требуется обеспечивать

, то

.

Таким образом, «платой» за переход от ФМ к ОФМ для устранения «обратной работы» является удвоение средней вероятности ошибочного приема.

На рис. 6.30 приведены кривые помехоустойчивости когерентного приема в двоичных системах, рассчитанные по выше полученным формулам.

Контрольные вопросы

1.        Как количественно оценивают помехоустойчивость систем передачи дискретных сообщений (СПДС)?

2.        Сформулируйте задачу расчета потенциальной помехоустойчивости СПДС.

3.        Напишите алгоритм оптимального когерентного демодулятора двоичной системы связи.

4.        Нарисуйте схему оптимального когерентного демодулятора АМ сигналов.

5.        Нарисуйте схему оптимального когерентного демодулятора ЧМ сигналов.

6.        Нарисуйте схему оптимального когерентного демодулятора ФМ сигналов.

7.        Изложите методологию расчета средней вероятности ощибочного приема в двоичной системе связи.

8.        От чего зависит помехоустойчивость двоичной системы связи?

9.        Приведите формулу расчета средней вероятности ошибочного приема АМ сигналов в двоичной СПДС.

10.    Приведите формулу расчета средней вероятности ошибочного приема ЧМ сигналов в двоичной СПДС.

11.    Приведите формулу расчета средней вероятности ошибочного приема ФМ сигналов в двоичной СПДС.

12.    В каком соотношении находятся энергии (мощности) сигналов с разными видами цифровой модуляции, обеспечивающие одинаковую помехоустойчивость? Дайте геометрическую трактовку этим соотношениям.

13.    Перечислите проблемы практического использования ФМ в СПДС.

14.    Что такое «обратная работа» и по каким причинам она возникает?

15.    В чем сущность ОФМ?

16.    Как формируют сигналы с ОФМ?

17.    Как осуществляют оптимальный когерентный прием с ОФМ?

18.    Как вычисляется средняя вероятность ошибочного приема в системах с ОФМ?

19.    Расположите системы с АМ, ЧМ, ФМ и ОФМ в порядке убывания помехоустойчивости при равных энергиях сигналов.

Рекомендации по проведению экспериментальных исследований

помехоустойчивости когерентного приема в двоичных СПДС

Для закрепления знаний, полученных при изучении разделов 6.4 и 6.5, целесообразно выполнить лабораторную работу № 17 «Исследование помехоустойчивости СПДС» в части, относящейся с когерентному приему (задания 1 и 2) (рис. 6.31, 6.32). Обратите внимание на близость экспериментальных оценок помехоустойчивости расчетным и на уменьшение их разброса с увеличением объема данных.

6.6. Синтез оптимального демодулятора в канале

с неопределенной фазой (некогерентный прием)

Постановка задачи:

Известны:

1. Ансамбль сигналов на выходе модулятора

{si(t)}m; i = 1, 2,…, m; t Î (0, T).

2. Непрерывный канал с неопределенной фазой

,

где t - случайная задержка сигнала в канале,

- случайная фаза с равномерным распределением

,

N(t) – квазибелый нормальный шум, т. е.

.

3. В качестве критерия качества приема используем критерий максимального правдоподобия (6.6), в котором отношение правдоподобия

, зависящее от Qk, является случайной величиной. Поэтому потребуем максимизации его математического ожидания

(6.24)

Требуется синтезировать оптимальный демодулятор, иначе говоря, найти алгоритм оптимальной обработки входного сигнала и принятия решения о передаваемом сообщении.

Решение

Исходя из ранее полученного выражения для Li (6.10), с учетом (6.13) можно записать

.

Для дальнейшего удобно сигнал разложить на квадратурные составляющие по углу Qk

Тогда

,

где

, (6.25)

.

Вернемся к отношению правдоподобия

.

Найдем математическое ожидание отношения правдоподобия (6.24)

.

Учитывая, что

– модифицированная функция Бесселя 0-го порядка, получим

.

Окончательно искомый алгоритм можно записать в виде

.

В таком виде алгоритм сложен для реализации. Для его упрощения можно применить любую монотонную функцию к выражению, стоящему в прямоугольных скобках [x], например, ln[x], что не изменит его суть

. (6.26)

Из алгоритма (6.26) вытекает схема демодулятора, показанная на рис. 6.33. Такая схема сложна для реализации, а сам алгоритм чувствителен к

. Снятие этой проблемы и упрощение схемы демодулятора возможно при выборе сигналов равных энергий Е1 = Е2 = ,,, = Еm, что обеспечивает равенство h1 = h2 = ,,, = hm. Это позволяет исключить в ветвях демодулятора сумматоры и нелинейные преобразователи со сложной монотонной функциональной характеристикой вида ln[I0(x)] (рис. 6.34), а алгоритм (6.26) принимает вид

(6.27)

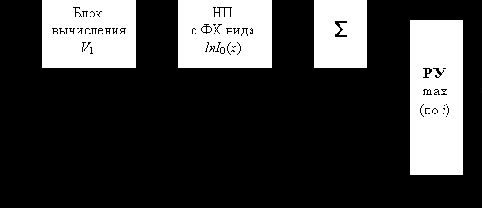
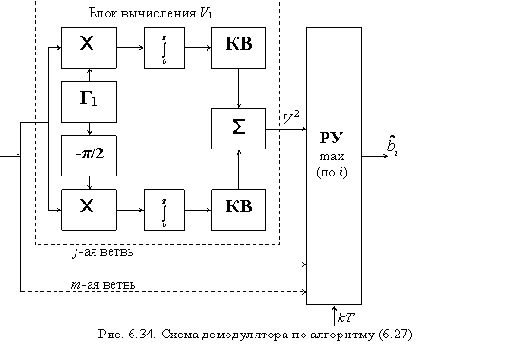
Способ приема сигналов, при котором не используется информация о его фазе, называют некогерентным, как и соответствующие демодуляторы. Его алгоритм был впервые получен Л.М.Финком.

Выше введенная функция Vi, как это следует из выражения (6.25), представляет собой не что иное, как огибающую реакции СФ для соответствующего сигнала si(t). Отсюда вытекает возможность реализации оптимального демодулятора, содержащего в каждой своей ветви СФ и детектор огибающей (ДО) (рис. 6.25). Решение о переданном символе принимается по максимум огибающей в моменты kT .

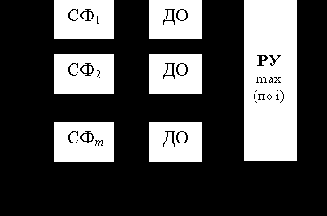
Из выражения (6. 25) очевидно, что максимальная помехоустойчивость некогерентного приема достигается при минимальном (нулевом) значении огибающей Vj (в моменты отсчетов) на выходах ветвей j ? i при передаче сигнала si(t). Для этого необходимо выбирать сигналы равных энергий, удовлетворяющие требованию ортогональности в усиленном смысле

.

Примеры ортогональных в усиленном смысле сигналов:

1. Сигналы с ЧМ при соответствующем выборе частот

.

2. Сигналы с время-импульсной модуляцией (ВИМ) (рис. 6.36,а)

.

3. Сигналы с ОФМ обладают ортогональностью в усиленном смысле на интервале –Т ÷ Т (рис. 6.36,б). На этом интервале сообщения «0» и «1» передаются сигналами:

Рекомендуется доказать ортогональность этих сигналов самостоятельно.

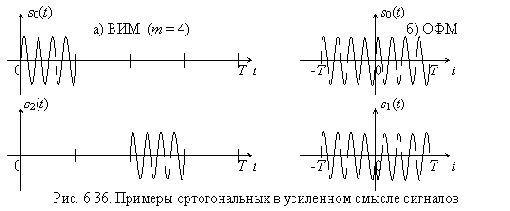
6.7. Потенциальная помехоустойчивость

некогерентного приема в двоичной системе связи

Для определения средней вероятности ошибки оптимального некогерентного приема в двоичной системе при равных вероятностях передаваемых сообщениях P(b0) = P(b1) достаточно вычислить условную вероятность ошибки любого типа, как это было установлено в разделе 6.4,

Вычислим

, ориентируясь на схему некогерентного демодулятора на СФ (рис. 6.37). Ошибка вида

(при передаче сообщения b1 принимается решение в пользу

) возникает, если для отсчетов огибающих на выходах ветвей демодулятора выполняется неравенство

. Для определения его вероятности

надо знать плотности вероятности

, вычислением которых и займемся.

Вспомним, что

,

где i – номер ветви ( индекс сигнала, на который настроен СФ)

,

j – индекс передаваемого сообщения.

.

Запишем отсчеты огибающих V0 и V1 на выходах соответствующих ветвей демодулятора при передаче сигнала s1(t) (j = 1)

i = 0

i = 1

.

Входящие в эти выражения скалярные произведения

представляют собой нормально распределенные случайные величины с нулевым математическим ожиданием, следовательно, огибающие Vi будут иметь распределение Рэлея на выходе СФ0 (i = 0)

и обобщенное распределение Рэлея на выходе СФ1 (i = 1)

.

Вернемся к вычислению средней вероятности ошибки при оптимальном некогерентном приеме

.

Произведя замену переменных

получим

.

Обозначим 2V1=V, 2?2 = g2, тогда

.

Здесь учтено то, что подынтегральное выражение можно трактовать как плотность вероятности обобщенного распределения Рэлея (5.13).

Вычислим ?2 – мощность шума на выходе СФ

и окончательно получим

,

где, как и ранее,

.

Полученный результат относится к любым двоичным системам, использующим ортогональные в усиленном смысле сигналы.

Нетрудно сообразить, что для некогерентного приема в двоичных системах с пассивной паузой (АМ)

Некогерентный прием сигналов с ФМ исключается, т.к. огибающие противоположных сигналов неразличимы, однако возможна реализация оптимального некогерентного демодулятора для системы с ОФМ (рис. 6.38), сигналы которой ортогональны в усиленном смысле на двойном интервале 2Т и, следовательно, имеют на этом интервале удвоенную энергию. По этой причине

.

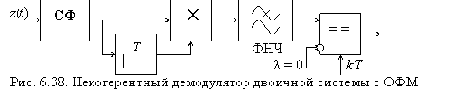
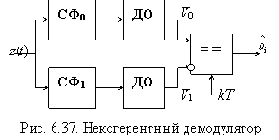
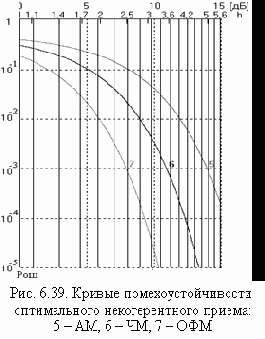
На рис. 6.39. приведены кривые помехоустойчивости оптимального некогерентного приема сигналов с АМ, ЧМ и ОФМ.

На практике используют также квазиоптимальный прием ЧМ сигналов, применяя в схеме (рис. 6.37) вместо СФ (согласованных с сигналами по их форме) полосовые фильтры (ПФ) с прямоугольной АЧХ, согласуя их с шириной спектра сигналов. В.И.Сифоровым было установлено, что максимальное отношение с/ш на выходе ПФ с прямоугольной АЧХ достигается при ширине полосы пропускания

и оно, естественно, несколько меньше, чем для СФ (энергетический проигрыш 0,86 дБ).

Дополнительное снижение помехоустойчивости при использовании ПФ вызывается межсимвольной интерференцией, возникающей из-за наложения переходных процессов от предшествующих посылок на последующие (что не имеет места при согласованной фильтрации).

Контрольные вопросы

1.     Сформулируйте задачу синтеза оптимального некогерентного демодулятора.

2.     Напишите алгоритм оптимального приема дискретных сообщений в канале с неопределенной фазой.

3.     Как упрощается алгоритм некогерентного приема при условии равенства энергий используемых сигналов?

4.     Нарисуйте схему оптимального некогерентного демодулятора для системы сигналов с разными энергиями.

5.     Нарисуйте схему оптимального некогерентного демодулятора для системы сигналов с равными энергиями.

6.     Как вычисляется огибающая Vi.

7.     Нарисуйте схему блока определения огибающей Vi.

8.     Нарисуйте схему оптимального некогерентного демодулятора на согласованных фильтрах.

9.     Что означает ортогональность сигналов в усиленном смысле?

10. Почему для достижения максимальной помехоустойчивости некогерентного приема требуется использование ортогональных в усиленном смысле сигналов?

11. Приведите примеры систем ортогональных в усиленном смысле сигналов.

12. При каких видах цифровой модуляции возможен некогерентный прием сигналов?

13. Изложите методологию расчета средней вероятности ошибок при оптимальном некогерентном приеме.

14. Почему возможен некогерентный прием сигналов с ОФМ, а с ФМ – нет?

15. Приведите формулы для вычисления средней вероятности ошибочного некогерентного приема АМ, ЧМ и ОФМ сигналов.

16. Что называют квазиоптимальным некогерентным приемом? В чем его достоинства и недостатки?

Рекомендации по проведению экспериментальных

исследований некогерентного приема

Для закрепления знаний, полученных при изучении разделов 6.6 и 6.7, целесообразно выполнить лабораторные работы № 16 «Исследование некогерентных демодуляторов» (рис. 6.40, 6.41) и № 17 «Исследование помехоустойчивости СПДС» в части, относящейся с некогерентному оптимальному и квазиоптимальному приему (задания 3 и 4) (рис. 6.42, 6.43).

Обратите внимание на инвариантность результатов некогерентного приема к фазовым сдвигам сигнала в линии связи. Убедитесь в снижении помехоустойчивости некогерентного приема по отношению к когерентному.

ЛИТЕРАТУРА

1.      Теория электрической связи: Учебник для вузов / А.Г.Зюко, Д.Д.Кловский, В.И.Коржик, М.В.Назаров; Под ред. Д.Д.Кловского.–М.:Радио и связь, 1998.–432 с.: ил.

2.      Радиотехнические системы передачи информации: Учеб. пособие для вузов / В.А.Борисов, В.В.Калмыков, Я.М.Ковальчук и др.; Под ред. В.В.Калмыкова. –М.: Радио и связь, 1990. –304 с.: ил.

3.      Теория передачи сигналов: Учебник для вузов / А.Г.Зюко, Д.Д.Кловский, М.В.Назаров, Л.М.Финк. – 2-е изд., переаб. И доп. – М.: Радио и сязь, 1986. – 304 с.: ил.;

4.      Сальников А.П. Теория электрической связи: Конспект лекций. Часть 1/ СПбГУТ. – СПб, 2002. – 109 с.: ил.

5.      Сальников А.П. Виртуальная учебная лаборатория по курсам кафедры теоретических основ связи и радиотехники / СПбГУТ.-СПб,2001.-100 с.: ил.

Содержание раздела

Главная сайта